Short Tutorial on Waveguides
Here I present the main theory of guided electromagnetic structures. The first section deals with a generic system. The main result of this section is represented by equation (8), which is an eigenvalue problem. This was made possible by the direct decomposition of the wave equation operator (i.e, the d’Almbertian) in time and then in the direction of propagation. Hence we end up with a simpler equation for the magnetic field, where now the 2D Laplacian operator operates on the magnetic field vector.
The eigenvalue problem can be simplified further in homogeneous media to transverse electric (TE) and transverse magnetic (TM) modes. This simplification allows the equation to be turned to an eigenvalue problem on a scalar field which is the longitudinal component of the magnetic in case of TE or electric in case of TM. I then show basic results of how tangential fields can be calculated and introduce the important concept of wave impedance.
The solution of the TE eigenvalue problem for cylindrical dielectric-coated circular wave guides is discussed in detail. Next, I spend some time discussing the concepts of reflections and transmissions in waveguides. An important takeaway point is the use of the transmission line model as a platform to describe interactions between waves in cascaded waveguides.
This tutorial will be updated regularly and may be split into two or more tutorials to make it easier for readers to digest and appreciate the theory.
An arbitrary cylindrical waveguide
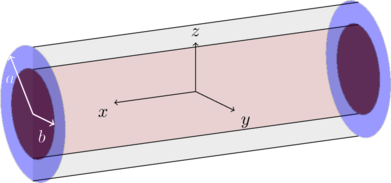
In this section we will derive the wave equation, fields expressions and the mode impedance of an arbitrary cylindrical waveguide. In this case the waveguide cross section can be of an arbitrary shape (not necessarily circular), and is uniform in the longitudinal direction.
Starting from the Curl equations and assuming no sources are present in the structure (i.e, ![]() ,
, ![]() )
)
(1) ![]()
and
(2) ![]()
Taking the curl of (2) and substituting in (1)
(3) ![]()
In regions where ![]() and
and ![]() are constant, the above equation become
are constant, the above equation become
(4) ![]()
where ![]() is the speed of the wave in the medium. Therefore
is the speed of the wave in the medium. Therefore
(5) ![]()
where
![]()
is the d’Almbertian (4-D Laplacian operator). Mathematically, ![]() in equation (??) can be interpreted as the vector fields that belong to the null space of
in equation (??) can be interpreted as the vector fields that belong to the null space of ![]() . To find possible
. To find possible ![]() , we decompose
, we decompose ![]() as
as
(6) ![]()
where ![]() is the 2D transverse Laplacian (
is the 2D transverse Laplacian (![]() plane in the above figure). We then seek solutions that are the eigenfunctions of the different components of
plane in the above figure). We then seek solutions that are the eigenfunctions of the different components of ![]() (This approach is the same as separation of variables, but presented from a different perspective.) For instance
(This approach is the same as separation of variables, but presented from a different perspective.) For instance ![]() has eigenfunctions that can be written as
has eigenfunctions that can be written as ![]() , where the corresponding eigenvalue is
, where the corresponding eigenvalue is ![]() . Plugging the eigenfunction of the second time derivative in Eq. (??) results in the time independent wave equation
. Plugging the eigenfunction of the second time derivative in Eq. (??) results in the time independent wave equation
(7) ![]()
where ![]() is the wavenumber inside the material, which is related to the free space wavenumber
is the wavenumber inside the material, which is related to the free space wavenumber ![]() by
by ![]() . (This is the wavenumber of an unbounded wave; it is not to be confused with the propagation wavenumber
. (This is the wavenumber of an unbounded wave; it is not to be confused with the propagation wavenumber ![]() that will be shown later to represent propagation in the
that will be shown later to represent propagation in the ![]() direction.) Similarly
direction.) Similarly ![]() is an eigenfunction of
is an eigenfunction of ![]() . Therefore,
. Therefore,
(8) ![]()
where ![]() . Note that (8) is a vector wave equation, where all the three components
. Note that (8) is a vector wave equation, where all the three components ![]() ,
, ![]() and
and ![]() satisfy it.
satisfy it.
Transverse Electric (TE) Waves
Two important classes of solutions to (8) are the Transverse Electric (![]() ) and transverse magnetic (
) and transverse magnetic (![]() ). For TE waves it is sufficient to solve Eqn. (8) for
). For TE waves it is sufficient to solve Eqn. (8) for ![]() and subsequently calculate the tangential component
and subsequently calculate the tangential component ![]() as (Classical Electromagnetic Theory, J. Vanderlinde, 2006)
as (Classical Electromagnetic Theory, J. Vanderlinde, 2006)
(9) ![]()
and the ![]() fields as
fields as
(10) ![]()
Additionally the wave impedance ![]() is
is
(11) ![]()
Here ![]() is the guided wavelength (i.e, wavelength in the
is the guided wavelength (i.e, wavelength in the ![]() direction).
direction).
Note that:
- The previous analysis is valid for an arbitrary cross section.
- Cut-off is defined as the frequency where a wave starts to propagate; for lower frequencies the fields exponentially decay.
-
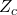 is imaginary below cut-off.
is imaginary below cut-off. - For a wave traveling in the
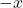 direction,
direction, 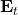 stays the same, while
stays the same, while 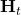 reverses direction (
reverses direction (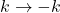 ). Hence, the complex Poynting vector
). Hence, the complex Poynting vector 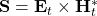 changes direction.
changes direction.
Example: Dielectric Coated Waveguide
Please refer to the first figure where we now consider the cross section to be circular. The core is a dielectric material with a dielectric constant ![]() and a radius
and a radius ![]() . The core is coated by another dielectric material with a dielectric constant
. The core is coated by another dielectric material with a dielectric constant ![]() and has a thickness
and has a thickness ![]() . Due to Azimuthal symmery, it is convenient to represent
. Due to Azimuthal symmery, it is convenient to represent ![]() in polar coordinates,
in polar coordinates,
(12) ![]()
Therefore, Eq. (8) becomes
(13) ![]()
We follow our decomposition procedure and decompose ![]() into the eigenfunctions of
into the eigenfunctions of ![]() , which are nothing but of the form
, which are nothing but of the form ![]() . Since
. Since ![]() and
and ![]() represent the same point,
represent the same point, ![]() must be an integer. Therefore letting
must be an integer. Therefore letting ![]() one gets
one gets
(14) ![]()
As previously mentioned, it is sufficient to solve for the ![]() component,
component, ![]() . Therefore for the
. Therefore for the ![]() component, Eq. (14) can be re-written as
component, Eq. (14) can be re-written as
(15) ![]()
Letting ![]() , Eq. (15) reduces to
, Eq. (15) reduces to
(16) ![]()
which is nothing but Bessel’s equation. Eqn. (16) has the general solution
(17) ![]()
or in terms of ![]() as
as
(18) ![]()
Here ![]() and
and ![]() are Bessel and Neumann functions, respectively.
are Bessel and Neumann functions, respectively.
The most general solution of ![]() assumes the form
assumes the form
(19) 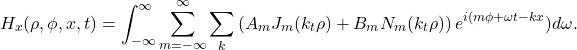
Note that ![]() and consequently
and consequently ![]() will be functions of the frequency
will be functions of the frequency ![]() and the angular modal number
and the angular modal number ![]() as will be determined from the dispersion relation as shown next. For azimuthally symmetric modes
as will be determined from the dispersion relation as shown next. For azimuthally symmetric modes ![]() , (19) becomes
, (19) becomes
(20) ![]()
For region 1, where ![]() and
and ![]() ,
, ![]() because
because ![]() is singular at the origin. Therefore at a given frequency
is singular at the origin. Therefore at a given frequency ![]() ,
,
(21) ![]()
where ![]() and in regions 2, where
and in regions 2, where ![]()
(22) ![]()
where ![]() . The tangential electric and magnetic fields can be calculated from Eqs. (10) and (9), respectively, where
. The tangential electric and magnetic fields can be calculated from Eqs. (10) and (9), respectively, where
(23) 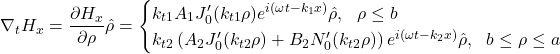
(24) 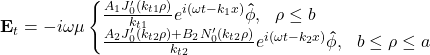
(25) 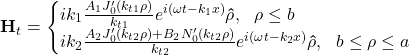
Boundary Conditions
At the interface ![]() ,
, ![]() ,
, ![]() and
and ![]() are continuous. Enforcing the continuity of
are continuous. Enforcing the continuity of ![]() , i.e,
, i.e, ![]() dictates that
dictates that ![]() . This can be understood by noting that for different values of
. This can be understood by noting that for different values of ![]() ,
, ![]() form coefficients of a system of homogeneous linear equations. Since
form coefficients of a system of homogeneous linear equations. Since ![]() is a real number, these coefficients, if
is a real number, these coefficients, if ![]() can be chosen to be independent, resulting in a trivial solution where
can be chosen to be independent, resulting in a trivial solution where ![]() ,
, ![]() and
and ![]() vanish. Therefore, it must be the case that for a given
vanish. Therefore, it must be the case that for a given ![]() ,
, ![]() , where
, where ![]() is a constant (i.e, the two columns of coefficient matrix are dependent). The constant
is a constant (i.e, the two columns of coefficient matrix are dependent). The constant ![]() can be absorbed in
can be absorbed in ![]() and
and ![]() . Hence
. Hence ![]() . Additionally,
. Additionally,
(26) ![]()
The continuity of ![]() (or
(or ![]() ) leads to
) leads to
(27) ![]()
Additionally at ![]() ,
, ![]() . Therefore,
. Therefore,
(28) ![]()
Note that ![]() can be set arbitrary. With no loss of generality, we will set
can be set arbitrary. With no loss of generality, we will set ![]() to unity.
to unity.
From (28)
(29) ![]()
Substituting (29) in (26) and (28) results in
(30) ![]()
and
(31) ![]()
Therefore after dividing (30) by (31),
(32) ![]()
Note that for each frequency ![]() , the characteristic equation (32) is ultimately a function of
, the characteristic equation (32) is ultimately a function of ![]() \footnote{This is because
\footnote{This is because ![]() .}. Therefore, the characteristic function can be written as
.}. Therefore, the characteristic function can be written as ![]() . For a given frequency
. For a given frequency ![]() , Eq. (32) can be satisfied for an infinite number of
, Eq. (32) can be satisfied for an infinite number of ![]() . A
. A ![]() value along with
value along with ![]() (here is zero), identify the waveguidfe mode. Beyond a cut-off frequency
(here is zero), identify the waveguidfe mode. Beyond a cut-off frequency ![]() ,
, ![]() will be real. We will label the different values of
will be real. We will label the different values of ![]() ,
, ![]() by the order of their corresponding
by the order of their corresponding ![]() , such that
, such that ![]() . This means that mode 1 will be denoted by
. This means that mode 1 will be denoted by ![]() , mode 2 by
, mode 2 by ![]() , etc.
, etc.
When ![]() , the waveguide approaches the conventional air-core circular waveguide. Eq. (32) is reduced to
, the waveguide approaches the conventional air-core circular waveguide. Eq. (32) is reduced to
(33) ![]()
and ![]() , where
, where ![]() is the
is the ![]() root of
root of ![]() \footnote{Note that
\footnote{Note that ![]() .}. Furthermore, if the inner core is filled with the same dieletric constant as the coating (i,e, the waveguide is completely filled),
.}. Furthermore, if the inner core is filled with the same dieletric constant as the coating (i,e, the waveguide is completely filled), ![]() and (33) also follows. Note that in both cases,
and (33) also follows. Note that in both cases, ![]() does not depend on frequency. Hence when two waveguides (completely) filled with two different dielectric materials
does not depend on frequency. Hence when two waveguides (completely) filled with two different dielectric materials ![]() and
and ![]() are cascaded, the
are cascaded, the ![]() modes will have the same radial profile. This implies that the tangential fields at their common interface match and the cascade can be described using transmission lines.
modes will have the same radial profile. This implies that the tangential fields at their common interface match and the cascade can be described using transmission lines.
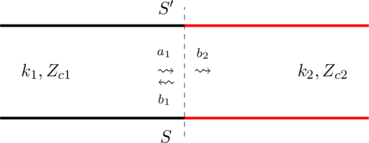
Cascade of Two waveguides
The figure below shows two cascaded waveguides that, in general, have different ![]() values. The dispersion relation
values. The dispersion relation ![]() of the waveguides and consequently the transverse wavenumbers
of the waveguides and consequently the transverse wavenumbers ![]() . Hence in the general case, the continuity of
. Hence in the general case, the continuity of ![]() and
and ![]() at the common interface
at the common interface ![]() cannot be satisfied for a single
cannot be satisfied for a single ![]() mode. In the following discussion, we will deterimne the condition at which
mode. In the following discussion, we will deterimne the condition at which ![]() and
and ![]() are equal; thus allowing the application of transmission line theory.
are equal; thus allowing the application of transmission line theory.

Cascade of two waveguides
In the most general setting, we allow the different ![]() values to be arbitrary. Enforcing
values to be arbitrary. Enforcing ![]() and
and ![]() to be equal implies that
to be equal implies that
(34) 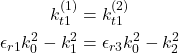
and
(35) 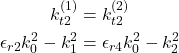
must be simultaneously satisfied. Therefore
(36) ![]()
which means that
(37) ![]()
In the subsequent analysis, we are interested in the special case where ![]() and WG1 is operating at cut-off (i.e,
and WG1 is operating at cut-off (i.e, ![]() ). Therefore
). Therefore
(38) ![]()
Additionally, the characteristic impedances ![]() and
and ![]() can be found using (11) to be
can be found using (11) to be
(39) ![]()
Therefore the propagation under the condition (36) can be described by the transmission line model shown in the figure below.