A given vector field ![]() with second derivatives can be decomposed as
with second derivatives can be decomposed as
(1) ![]()
where ![]() is a scalar field and
is a scalar field and ![]() is a vector field. Additionally,
is a vector field. Additionally,
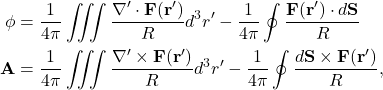
where ![]() .
.
To prove Helmholtz theorm, we use the following indentities
(2) ![]()
Additionally if ![]() is not a function of
is not a function of ![]() then
then
(3) ![]()
which may appear to be too obvious to explicitly mention since ![]() is not a function of
is not a function of ![]() . However, it should be noted that the LHS Laplacian operates on a vector field, while the RHS one operates on a scalar function. To proof the above identity, we use the definition of Laplacian of a vector:
. However, it should be noted that the LHS Laplacian operates on a vector field, while the RHS one operates on a scalar function. To proof the above identity, we use the definition of Laplacian of a vector:
(4) ![]()
Replacing ![]() by
by ![]() one gets
one gets
(5) 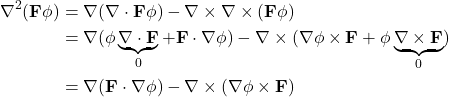
Using the identity:
![]()
and noting that ![]() does not on
does not on ![]() and that
and that ![]() ,
,
(6) ![]()
Furthermore we use the following identity to simplify the second term
![]()
Therefore,
(7) ![]()
This means that
(8) ![]()
Now we are ready to start the prove of Helmholtz theorem.
(9) 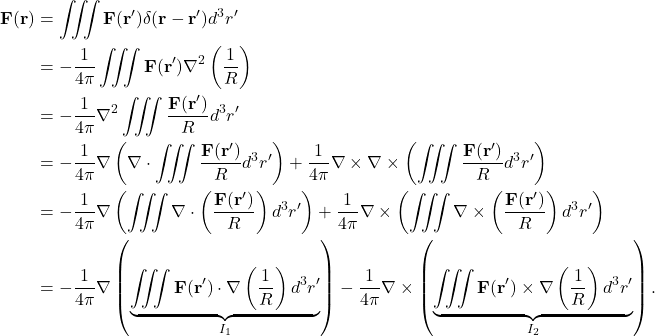
Note that
![]()
Therefore,
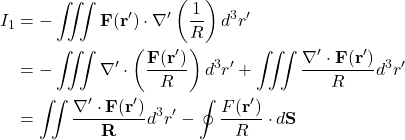
and
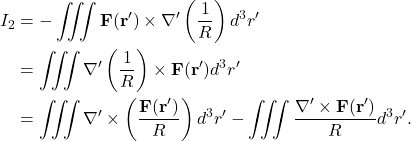
We know that
![]()
therefore,
![]()
If we let
![]()
and
![]()
we get
![]()