Introduction
In this short article, we will make the connection between the electromagnetic fields and matter more complete. The discussion is basically classical (matter obeys Newtonian mechanics).
Background
With the appropriate choice of units Maxwell’s equations in free space can be written as
(1) 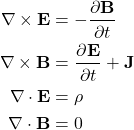
We consider these four equations to be the most fundamental. Furthermore ![]() and
and ![]() are the principle quantities. When matter is present, it will exhibit itself via its charge motion which appears in the quantities
are the principle quantities. When matter is present, it will exhibit itself via its charge motion which appears in the quantities ![]() and
and ![]() . Indeed from an electromagnetic theory perspective, matter is nothing but charges.
. Indeed from an electromagnetic theory perspective, matter is nothing but charges.
Closing the loop: Lorentz Force
As we see from the above equations, the motion of charges change the fields. So far we have not considered the other direction: The effect of the fields on the charges. The fields act upon the charges by a special force known as the Lorentz force
(2) ![]()
where ![]() is the velocity of the charge
is the velocity of the charge ![]() . Given
. Given ![]() and all other mechanical forces acting on
and all other mechanical forces acting on ![]() ,
, ![]() moves according to Newton’s law
moves according to Newton’s law
(3) ![]()
As the charge trajectory changes under the influence of ![]() (
(![]() is part of it), the charge distribution
is part of it), the charge distribution ![]() and current density
and current density ![]() changes and consequently the fields.
changes and consequently the fields.

In the most general setting Maxwell’s equations and Lorentz force summarize all of classical physics (if we do not consider Newton’s gravitational law, which is also a fundamental law).
Eulerian vs Lagrangian Paradigms
Note that Maxwell’s equations adopt the Eulerian perspective, where the main interest is on volumes in space and how quantities flow through their boundaries. On the other hand, Newton’s second law allows us to track specific particles and hence adopts the Lagrangian perspective. I will talk later about how to assimilate the two perspectives when discussing Maxwell’s stress tensor.
A piece of matter contains hundreds of millions of charged particles that affect one another and are affected by the electromagnetic field. Such interactions are quite complex. In principle, we can describe matter by applying Newton’s law (and include Lorentz force ![]() ) for every particle. We then go and solve Newton’s second law coupled with Maxwell’s equations. Practically, the process can be daunting. Fortunately, the response of a wide class of materials to the electromagnetic fields (i.e, the collective response under the influence of Lorentz force) can be lumped in a set of parameters that we call the effective (constituitive) parameters. In the next article I will shed light on three important classes of matter: Dielectrics, Conductors and Magnetics.
) for every particle. We then go and solve Newton’s second law coupled with Maxwell’s equations. Practically, the process can be daunting. Fortunately, the response of a wide class of materials to the electromagnetic fields (i.e, the collective response under the influence of Lorentz force) can be lumped in a set of parameters that we call the effective (constituitive) parameters. In the next article I will shed light on three important classes of matter: Dielectrics, Conductors and Magnetics.