Maxwell’s equations in 2D
Consider a system that is infinitely long in the ![]() direction such that
direction such that ![]() . Therefore Maxwell’s equations reduce to
. Therefore Maxwell’s equations reduce to
(1) 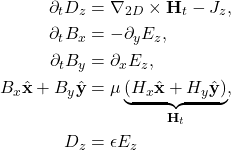
(2) 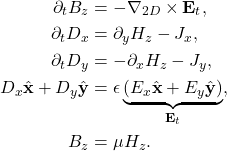
![]() is the 2D curl operation, which is equal to
is the 2D curl operation, which is equal to
(3) ![]()
Note that in the 2D case, Maxwell’s equations split into two decoupled systems as shown by the above two systems of equations. The first (second) system is called the TM (TE) mode since ![]() (
(![]() ).
).
Wave Equation
For the TM mode, we can eliminate the magnetic field ![]() to get the wave equation
to get the wave equation
(4) ![]()
where
![]()
Similarly the wave equation of the TE assumes the form
(5) ![]()
Normal (eigen) modes
When the source term ![]() or
or ![]() is zero then we end up with the homogeneous wave equation:
is zero then we end up with the homogeneous wave equation:
(6) ![]()
If we consider fields that sinusoidally vary with time (i.e., ![]() ) then we end up with the following eigenvalue problem
) then we end up with the following eigenvalue problem
(7) ![]()
If we consider the structure to be an infinitely long with a rectangular cross section as shown below, where the orange lines represent conducting boundaries. For the TM mode this means that:
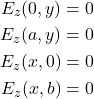
\centering
It can shown that for the TM mode, ![]() can be written as
can be written as
(8) ![]()
where
![]()
,
![]()
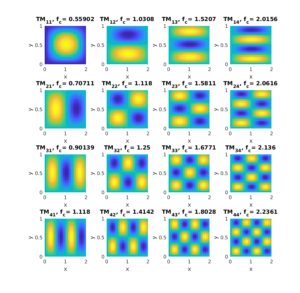
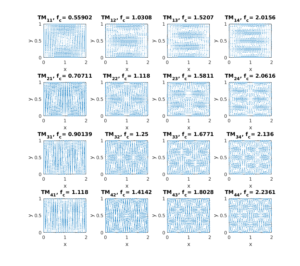
where ![]() is the mode number. A mode is identified by its mode number. Therefore it is convenient to write the mode as
is the mode number. A mode is identified by its mode number. Therefore it is convenient to write the mode as ![]() , which has a resonant frequency:
, which has a resonant frequency:
(9) ![]()
where again I used the normalized unit (![]() ). I also considered the case where the cavity is filled with air. The figure below plots the fields of the first 20 modes (
). I also considered the case where the cavity is filled with air. The figure below plots the fields of the first 20 modes (![]() ).
).
Mode Excitation
For this animation, I made the cross section to be square. In the first case the length of the square was set to ![]() to make sure that the resonant frequency of the
to make sure that the resonant frequency of the ![]() mode is 1 unit. In the second example, the length was changed to
mode is 1 unit. In the second example, the length was changed to ![]() such that the resonant frequency of the
such that the resonant frequency of the ![]() or
or ![]() modes to be unity.
modes to be unity.
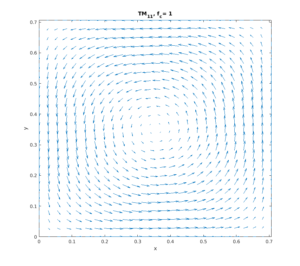
Note that the mode strength increases as the source approached the center of the cavity. By inspecting the profile of the magnetic field of the TM11 mode shown below, it is clear that the magnetic fields “circulates around the center. This means that according to Ampere’s law, when the current source moves to the center, it excites the magnetic field and subsequently the electric field. Note also that the field strength does not change even when the source leaves the center and moves toward the edges. The reason behind this is related to the Quality factor of the mode. The cavity walls were made from a high conductivity material, which means that the fields sustain over time.
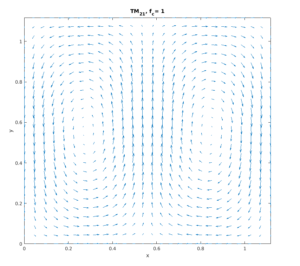
For the ![]() mode, the
mode, the ![]() factor was made to be 100 times less (hence allowing the mode to dissipate much faster). Note from the plot below of the magnetic field that the maximum excitation is expected when the source moves toward the magnetic fields nulls as the next animation shows.
factor was made to be 100 times less (hence allowing the mode to dissipate much faster). Note from the plot below of the magnetic field that the maximum excitation is expected when the source moves toward the magnetic fields nulls as the next animation shows.