Electromagnetism as a Dynamic System

Introduction

One of the main challenges in understanding the electromagnetic phenomenon is not appreciating what Maxwell’s equations entail. One reason behind this is the easiness of getting lost in the mathematical details. Another reason is the focus on the solution techniques more than on the big picture. The second reason in particular is very common when studying engineering electromagnetism. Students usually focus more on the different techniques (solution of boundary value problems, eigenmodes calculations, fields or radiating elements, transmission lines, etc) more than they focus on the rationale behind applying a particular technique to solve a specific set of problems.

In this following sections, we go one step back and ask the important question: What do Maxwell’s equation actually solve?

Newtonian Mechanics

If we make a contrast between Newtonian mechanics and electromagnetism, we clearly see that most students will have a better understanding of the big picture in Newtonian mechanics. Students are introduced to Newton’s second law

$\mathbf{F}_{net}=\frac{d\mathbf{P}}{dt}=m\mathbf{a}.$

The main problem solved in mechanics is the finding of the trajectory $\mathbf{r}$ of a particle or a system of particles as the system evolves under the influence of applied forces with a resultant $\mathbf{F}_{net}$ . Since

$\mathbf{a}=\frac{d^2\mathbf{r}}{dt^2},$

then we integrate the above equations twice to find the trajectory $\mathbf{r}$ as a function of time. Calculus and the theory of differential equations become a necessary tool that provide us with the techniques to find $\mathbf{r}$ . Additionally, the theory supplies us with the conditions required to integrate Newton’s law: the initial conditions. Indeed we know that we need to specify $\mathbf{r}$ and its rate of change (i.e, the velocity) $\dot{\mathbf{r}}$ at a given time instant $t_0$ then calculate the position and velocity at any other time $t$ .

System States

The theory of differential equations provides us with useful tools and techniques that can be employed to find the system’s trajectories. Not only this, it also exposes the algebraic structure of the solution. Indeed, the system is reduced to the evolution of a state vector $\mathbf{x}$ that lives in a mathematical vector space. Although this concept may appear to be abstract, it is very useful. In fact, it becomes of utmost importance in the field like Quantum mechanics. If we go back to the motion of a single particle under the influence of a net force $\mathbf{F}_{net}$ , the state vector becomes the tuple $\mathbf{x}=[\mathbf{r},\dot{\mathbf{r}}]$ . This vector, visualized in the abstract mathematical dynamically rotates and change size as time goes.

If the number of particles increases, the dimension of the mathematical space increases but the basic principle is still the same: the system stretches, compresses and rotates the state vector as time passes. Furthermore, for continuum media like strings and fluids the states become in-countably many and they form a continuum. In this case ordinary differential equations turns into partial differential equations; but the principle is still the same.

Evolution of the Fields

Maxwell’s equations in particular the two curl equations

$\begin{align*} \nabla\times \mathbf{E}&=-\frac{\partial \mathbf{B}}{\partial t}\\ \nabla\times \mathbf{B}&=\frac{\partial \mathbf{E}}{\partial t}+\mathbf{J} \end{align*}$

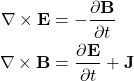
can be re-written as

(1) $\begin{equation*} \frac{\partial}{\partial t} \begin{bmatrix} \mathbf{E} \\ \mathbf{B} \end{bmatrix} =\underbrace{\begin{bmatrix} 0 & \nabla\times\\ -\nabla\times & 0 \end{bmatrix}}_\mathcal{L} \begin{bmatrix} \mathbf{E} \\ \mathbf{B} \end{bmatrix} +\begin{bmatrix} -\mathbf{J} \\ \mathbf{0} \end{bmatrix}. \end{equation*}$

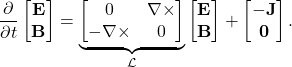
(In the above equations, I use the system of unit where $\epsilon_0=1$ , $\mu_0=1$ ). The above equation symbolically represents a dynamical system $\dot{\mathbf{x}}=A\mathbf{x}+B\mathbf{u}$ , where the states are $\mathbf{E}$ and $\mathbf{B}$ that form a continuum. The operator $\mathcal{L}$ is equivalent to the matrix $A$ . In a discretized version of the above equation, the curl operators $\nabla\times$ appearing in $\mathcal{L}$ couple near states together.

So far we have only considered the curl equations. Nevertheless Helmholtz’s theorem (a proof is shown here) states that to describe a vector field both the curl and the divergence of the field must be specified. Note that if $\nabla\cdot\mathbf{B}$ is zero at some time $t_0$ then the evolution equation (basically Faraday’s law) guarantees that $\nabla\cdot\mathbf{B}=0$ for all other times.

Furthermore, if at some time $t_0$ , $\nabla\cdot\mathbf{E}(t_0)=\rho(t_0)$ then Ampere’s law along with charge conservation guarantee that $\nabla\cdot\mathbf{E}(t)=\rho(t)$ for any other time interval.

The above arguments give us what Maxwell’s equations really calculate: the evolution of the fields (states) $\mathbf{E}$ and $\mathbf{B}$ from $t_0$ to any other time $t$ such that

(2) $\begin{equation*} \nabla\cdot\mathbf{B}(t_0)=0 \end{equation*}$

and

(3) $\begin{equation*} \nabla\cdot\mathbf{E}(t_0)=\rho(t_0). \end{equation*}$

Strictly speaking, Maxwell’s equations do not determine the fields; they determine their evolution over time once they are known at some time $t_0$ . The four equations are mathematically consistent such that the fields at any other subsequent time $t$ satisfy the charge conservation principle.

References

H. Haus, J. Melcher, “Electromagnetic Fields and Energy“.

Electromagnetism as a dynamic system